Научный электронный журнал КубГАУ . № 02(2), 2003
УДК 539.3:534:532.5
Эволюционное уравнение продольных уединенных волн в вязкоупругой бесконечной пластине и его точное решение
Аршинов Г.А. – канд. физ.-мат. наук, доцент
Кубанский государственный аграрный университет
Выводятся уравнения движения геометрически нелинейной вязкоупругой пластины, используются неклассические кинематические уравнения. Рассмотрен общий случай, когда вязкоупругие свойства проявляются при объемных и сдвиговых деформациях. Полученные уравнения методом возмущений сводятся к эволюционному уравнению Кортевега де Вриза – Бюргерса – Петвиашвили, для которого определяется точное решение, описывающие продольные двумерные уединенные волны. Указываются условия, при которых формируются ударно-волновые структуры деформации пластины.
Уединенные нелинейные волны в нелинейных упругих пластинах исследуются в работе [1]. В работе [2] изучаются дисперсионные нелинейные волны в вязкоупругих пластинах при упругих объемных деформациях. В данной статье предлагается обобщение результатов, полученных в [2], когда вязкоупругие свойства пластины проявляются при объемных и сдвиговых деформациях.
Для исследования распространения нелинейных дисперсионных волн в бесконечной вязкоупругой пластине толщиной 2h, изготовленной из материала наследственного типа и свободной от внешних воздействий, построим математическую модель волнового процесса.
С помощью кинематических соотношений определим компоненты вектора перемещений точек пластины при симметричных по толщине колебаниях и невысоких частотах [2]
v
;
, (1)
где 
и v
- функции, определяющие поле перемещений в срединной плоскости пластины
соответственно по осям 
и 
,
- перемещения по оси z, 
- время.
Конечные деформации пластины зададим соотношениями тензора Грина
(2)
предполагая, что 
, 
.
Воспользуемся уравнениями линейной вязкоупругости для описания наследственных реологических свойств пластины 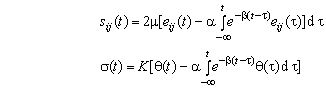[3]
, (3)
где 
- соответственно компоненты девиаторов напряжений и
деформаций; 
− среднее напряжение, 
- объемное расширение, 
− модуль объемной деформации,
- параметр
Ламе; 
- константы, определяющие реологические
свойства стержня; Е - модуль Юнга;
- коэффициент Пуассона.
С помощью формулы (1) определим компоненты деформаций по формулам
(2) и их вариации 
. Из закона состояния (3) найдем компоненты
тензора напряжений 
.
Далее, руководствуясь вариационным принципом
,
где 
- плотность материала пластины, - вариации деформаций, 
- вариации перемещений, точкой обозначена производная
по времени,
получаем интегро-дифференциальные уравнения движения пластины:
= 
.
= 
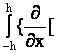
vx
vy)]
+ 
vy)
.
= 
(4)
+ 
+
,
где введены следующие обозначения:
, (5)
, (6)
- поправочный коэффициент.
Для наследственных материалов с быстро затухающей памятью, когда
, систему уравнений (4) можно упростить. Заменим в выражениях
(5) и (6) интегральные операторы дифференциальными, разлагая функции
, 
в ряды Тейлора по степеням (
) и сохраняя в полученных разложениях два слагаемых.
В итоге получим аппроксимации
, 
, (7)
где введены операторы
, 
,
действующие на функцию 
по правилу
, 
.
Введем ряд обозначений: А – амплитуда колебаний, l
– длина волны и 
– малый параметр, позволяющий исследовать длинные волны малой амплитуды.
Заменим в системе (4) 
и 
их приближениями (7) и перейдем к безразмерным переменным:
, v = 
v*, 
, 
, 
,
. (8)
Исследуем безразмерные уравнения движения пластины с помощью асимптотического метода. Неизвестные функции запишем в виде асимптотических разложений, опуская звездочки при соответствующих безразмерных переменных:
, v = 
(v1 + v2
+…), 
. (9)
Если величины , 
, 
– одного порядка малости, то разложения (9) можно подставить
в безразмерные уравнения движения пластины.
Обозначенные отношения порядков позволяют для первых членов разложений составить следующую систему уравнений:
(10)
= 0, (11)
из которой следует, что
, (12)
где 
, 
.
Скорость волны найдем исходя из уравнения (10) и с учетом формулы (12):
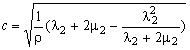. (13)
Далее для вторых членов разложений (9) составим систему трех уравнений:
v
+ 
(14)
v
= 
v
+ 
.
(15)
v
)+
. (16)
В ходе интегрирования уравнения (15) по переменной 
и с учетом формулы (12) получим равенство:
v
=
.
Принимая во внимание последнее равенство и формулу (12), продифференцируем
уравнение (16) по и приведем его к виду:
. (17)
Приравнивая сумму последних трех слагаемых в уравнении (14) к левой
части уравнения (17), умноженной на 
,
с учетом выражения (13) можно записать следующее:
v
+
+
.
В ходе тождественных преобразований последнего уравнения, используя
обозначение 
, получим эволюционное уравнение Кадомцева
– Петвиашвили – Бюргерса
, (18)
,
.
Найдем точное решение уравнения (18) из сингулярного многообразия вида:
, (19)
где 
– неизвестные функции независимых переменных.
В результате подстановки выражения (19) в уравнение Кадомцева – Петвиашвили – Бюргерса можно записать равенство:
, (20)
где 
удовлетворяет условию (20) и вычисляется следующим образом:
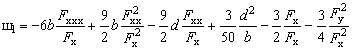. (21)
Подставив функцию 
в равенство (20), приходим к точному
решению уравнения КПБ:
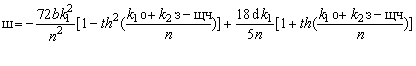, (22)
где 
– произвольный параметр, 
,
или
,
где
. (23)
Волну растяжения, соответствующую неравенству
, получим, если в формуле (23) оставим знак «+». При
этом 
и точное
решение уравнения Кадомцева – Петвиашвили – Бюргерса описывает ударно-волновую
структуру.
Возвращаясь к размерным переменным, запишем функцию
,
согласно которой найдем поправку к скорости распространения волны:
.
Список литературы
1. Потапов А.И. Нелинейные волны деформации в стержнях и пластинах. Горький: Изд-во Горьк. гос. ун-та, 1985.
2. Аршинов Г.А., Могилевич Л.И. Статические и динамические задачи вязкоупругости. Саратов: Изд-во СГАУ им. Н.И. Вавилова, 2002. 146 с.
3. Москвитин В.В. Сопротивление вязкоупругих материалов. М.: Наука, 1972.
Научный электронный журнал КубГАУ . № 02(2), 2003